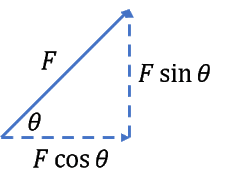Vectors are useful mathematical tools to describe physical quantities that contain both magnitude and direction.
Examples of such physical quantities are displacement, velocity, acceleration, forces, etc.
When students work with forces, teachers will teach them how to add force vectors using the parallelogram or the triangle method to find the resultant force.
These methods work well if there are only two forces are given.
What happens when there are more than two forces? We can teach students how to do the resolution of forces method.
The gist is like this:
- resolve all forces into their horizontal and vertical components,
- the horizontal /vertical component of the resultant force is the sum of all the horizontal/vertical components,
- the magnitude of the resultant force is obtained using Pythagoras’ theorem,
- the direction of the resultant force (angle from the positive x-axis) can be obtained using the following equation:
where the numerator and denominator are the y– and x-component of the resultant force (labeled R), respectively.
Using the following example:
If we want to add these 3 force vectors together (which is the resultant of these 3 forces), we find the horizontal and vertical components for each force, then we sum the components. Below is the table.
Now we have the horizontal and vertical components of the net force. We can find the magnitude and direction of the net force.
Direction: from the positive x-axis
I really like this method as I don’t need to worry about the exact drawing of vectors using the parallelogram or triangle method.
The next issue would be how to know when to use sine or cosine.
Here is how: after you drew the vector and identify the angle from the horizontal or vertical, a right-angle triangle can be traced out.
If the component is adjacent to the angle, you use the cosine. If the component is opposite to the angle, you use the sine.
Practice a few more times and you will become a vector resolution expert!